1876 mathematical proof by the US president

Garfield's proof of the Pythagorean theorem is an original proof of the Pythagorean theorem discovered by James A. Garfield (November 19, 1831 – September 19, 1881), the 20th president of the United States. The proof appeared in print in the New-England Journal of Education (Vol. 3, No.14, April 1, 1876).^[1][2] At the time of the publication of the proof Garfield was a congressman from Ohio. He assumed the office of President on March 4, 1881, and served in that position until his death on September 19, 1881, having succumbed to injuries sustained when he was shot in an assassination in July.^[3] Garfield is thus far the only President of the United States to have contributed anything original to mathematics. The proof is nontrivial and, according to the historian of mathematics William Dunham, "Garfield's is really a very clever proof."^[4] The proof appears as the 231st proof in The Pythagorean Proposition, a compendium of 370 different proofs of the Pythagorean theorem.^[5]

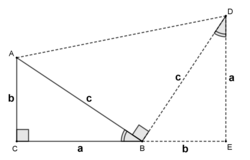
In the figure, ${\displaystyle ABC}$ is a right-angled triangle with right angle at ${\displaystyle C}$. The side-lengths of the triangle are ${\displaystyle a,b,c}$. Pythagorean theorem asserts that ${\displaystyle c^{2}=a^{2}+b^{2}}$.

To prove the theorem, Garfield drew a line through ${\displaystyle B}$ perpendicular to ${\displaystyle AB}$ and on this line chose a point ${\displaystyle D}$ such that ${\displaystyle BD=BA}$. Then, from ${\displaystyle D}$ he dropped a perpendicular ${\displaystyle DE}$ upon the extended line ${\displaystyle CB}$. From the figure, one can easily see that the triangles ${\displaystyle ABC}$ and ${\displaystyle BDE}$ are congruent. Since ${\displaystyle AC}$ and ${\displaystyle DE}$ are both perpendicular to ${\displaystyle CE}$, they are parallel and so the quadrilateral ${\displaystyle ACED}$ is a trapezoid. The theorem is proved by computing the area of this trapezoid in two different ways.

${\displaystyle {\begin{aligned}{\text{area of trapezoid }}ACED&={\text{height}}\times {\text{average of parallel sides}}\\&=CE\times {\tfrac {1}{2}}(AC+DE)=(a+b)\times {\tfrac {1}{2}}(a+b)\end{aligned}}}$.

${\displaystyle {\begin{aligned}{\text{area of trapezoid }}ACED&={\text{area of }}\Delta ACB+{\text{area of }}\Delta ABD+{\text{area of }}\Delta BDE\\&={\tfrac {1}{2}}(a\times b)+{\tfrac {1}{2}}(c\times c)+{\tfrac {1}{2}}(a\times b)\end{aligned}}}$

From these one gets

${\displaystyle (a+b)\times {\tfrac {1}{2}}(a+b)={\tfrac {1}{2}}(a\times b)+{\tfrac {1}{2}}(c\times c)+{\tfrac {1}{2}}(a\times b)}$

which on simplification yields

${\displaystyle a^{2}+b^{2}=c^{2}}$