I’ve traveled to Xi’an to play with my friend, Zambon21. There are some boring time which must be passed, and so we tried to pass them using brain-procedurally generated simplified D&D-like campaigns. As all D&D campaigns requires dice, ours is no exception. But by then we were presented with no other tools except our mortal bodies (because both of our phone’s batteries had run out), and mortal bodies are quite bad at generating random numbers. Inspiration struck when we wandered straight into a tourist trap. Exploiting the polar coordinate, we thought up a neat little trick to generate random numbers, and simplified it so that it can simulate a randomly generated die roll. Along with the method, we bundled a fun little game that can be played with no other tools other than the fake dice we invented above. After all, who doesn’t love random numbers?

Methodology

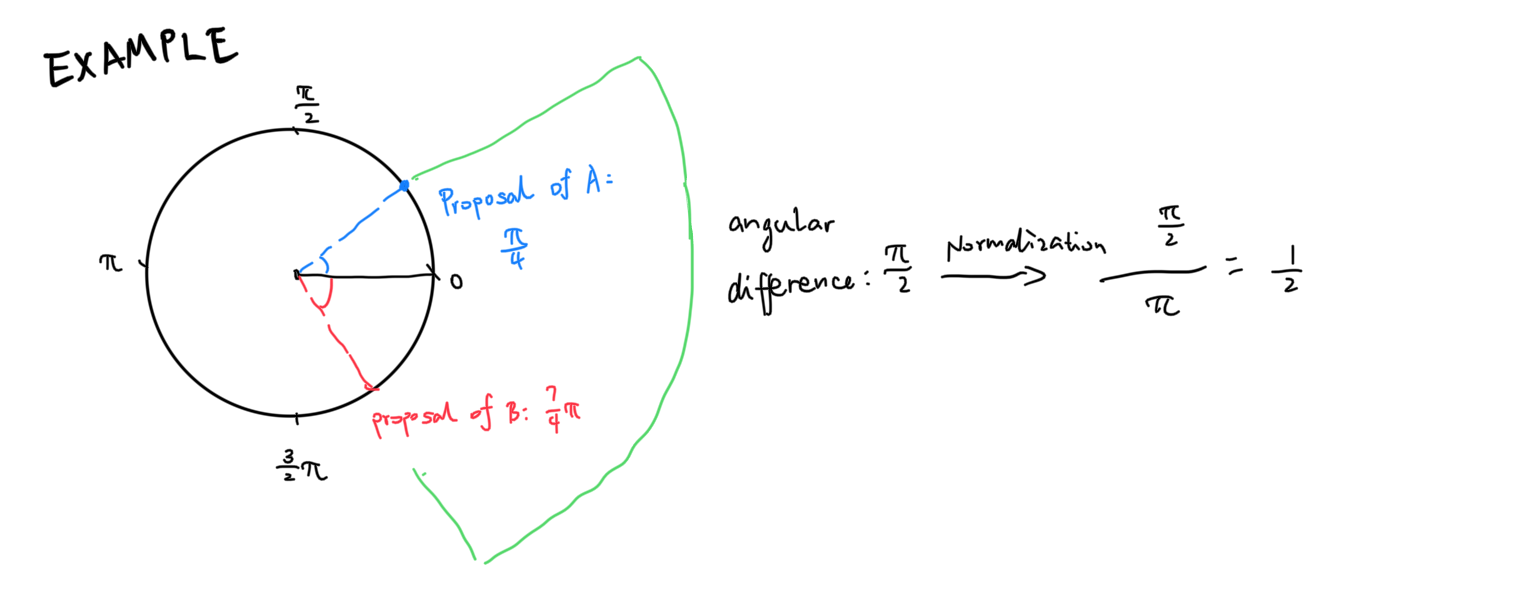
We will present the random number generation method below. The method is capable of generating numbers between \([0, 1)\) and requires the participation of two parties, and two positions situated on the unit circle of the polar coordinate system to work.

1. A number (\(\theta_1\)) is proposed by A.
2. Another number (\(\theta_2\)) is proposed by B.
3. The angular difference is evaluated (\(\delta\)).
4. The angular difference is normalized: \(\delta = \frac{\delta}{\pi}\).

If A and B are biased and are not capable of generating real random numbers on their own, but they have a conflict of interest, this will cause both A and B to try to maximize or minimize the angular difference, and therefore, producing a semi-random result. Cool!

If the difference \(\delta\) is bigger than \(\pi\), we invert it using \(\delta \rightarrow \delta - \pi\), so the RNG is always capped between 0 to 1.

Discretization

Obviously humans are very inept at generating continuous fake random numbers, and the method above is 1. not very intuitive and 2. not a die and therefore not usable in a vastly simplified D&D campaign. We simplified the algorithm so that both challenges can be solved.

First, we rotate the above polar coordinate by 90deg so that 0 is on the top. Then, we flip it along the y axis so it becomes clockwise. Basically, we turn it into a literal clock. We mark the circle with clock numbers as well.

Two parties come up with a number ranged between \([0, 12)\) simultaneously to avoid the information gap. We then measure their angular difference. For example, A comes up with 2 and B comes up with 10. The angular difference will be 4 in this case. The fake die roll result is then calculated using the angular difference.

---------------------------------
|  Angular Distance | Die roll  |
---------------------------------
|  0, 6             |    6      |
|  1                |    1      |
|  2                |    2      |
|  3                |    3      |
|  4                |    4      |
|  5                |    5      |
---------------------------------

We can prove that in an ideal situation, the die roll will be fair. Assuming both parties can come up with unbiased random numbers ranging from \([0, 12)\), we can always rewrite the clock numbers so that A is always situated at 0. This means \(P_A(0) = 1\), and the probability for the resulting distance now entirely depend on the probability of where B lands. This is due to something to the effect of distance is rotational invariant.

---------------------------------------------
| Distance    | Landing point | Probability |
---------------------------------------------
|   0         |       0       |   1/12      |
|   1         |     1, 11     |   1/6       |
|   2         |     2, 10     |   1/6       |
|   3         |     3, 9      |   1/6       |
|   4         |     4, 8      |   1/6       |
|   5         |     5, 7      |   1/6       |
|   6         |       6       |   1/12      |
---------------------------------------------

We don’t have to lock A to 0 - any party can become the anchor point. Due to the symmetry, it doesn’t really matter. The result will be the same. Distance 1-5 conveniently have the same probability with the probability of a die roll - \(\frac{1}{6}\); 0 and 6 not so much, with a probability of \(\frac{1}{12}\). As a result, we combine them together to mark the die roll of 6.

Experiment

We have written a little experiment in Lua to verify the things we said above.

diecount = {}

function propose() 
    return math.floor(math.random() * 12)
end

function wrap(x) 
    if x < 0 then 
        return x + 12
    end
    if x >= 12 then 
        return x - 12
    end
    return x
end

function pdistance(a, b)
    local lut = {
        0, 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1
    }
    return lut[wrap(b - a) + 1]
end

function roll()
    a = propose()
    b = propose()
    pt = pdistance(a, b)
    if pt == 0 then
        pt = 6
    end
    diecount[pt] = diecount[pt] + 1
end

By offsetting B with -A, we can evaluate the angular distance using a lookup table, which saves up to 2 ifs.

Here’s the statistics after executing the roll() function above for 1,000,000 times. A fair die should have equal probability for each side, that is, 1/6, or 16.66666…%:

--------------------------------
| Roll   | Count  |    %       |
--------------------------------
|  1     | 166390 |  16.639%   |
|  2     | 167068 |  16.7068%  |
|  3     | 166697 |  16.6697%  |
|  4     | 166385 |  16.6385%  |
|  5     | 166622 |  16.6622%  |
|  6     | 166838 |  16.6838%  |
--------------------------------

Verbal Tennis

Besides verbal D&D, me and my friend had come up with a little game based on the die roll: verbal tennis. In verbal tennis, each player starts with 3 points of stamina. When player 1 serves the ball, they can choose whether to spend stamina or not. Used bar of stamina will grow back after 3 turns. Player 1 and player 2 then says a random number together at the same time to generate a die number (a). Player 2 can only successfully return the ball if they get (a + stamina used) or above.

Just like player 1 can punish the die count by spending stamina, player 2 can award the die count by spending their stamina as well. Player 2 additionally have the option to spend stamina to punish player 1’s roll, should the ball be successfully returned. The game ends when one player wins using whatever tennis rules you guys choose to use. Here’s a very immaturely drawn comic strip demonstrating the game procedure.

Conclusion

That’s it! One neat little trick we’ve discovered to roll a die, without a die. The method is not without its flaw though. To at least make it fair, both participants will need to have opposite targets or interests, otherwise the roll result might be rigged. So one side must be actively trying to achieve the minimal roll, while the other side trying to maximize it. And of course, when there is an actual die in your possession, or you have things like Sophie’s Dice, this method becomes useless. The third downside is that the discretized method can only roll a d6; there might simply be too many numbers to track if you want to roll a d20. Finally, although this is not what this blog should be posting, conventionally speaking, I hope you guys had fun reading it. And of course, feel free to use it next time in your oversimplified D&D campaign!

Copyleft 2023 42yeah.