Let's take a look at the original approach, Denoising Diffusion Probabilistic Models. Newer advances build on the language and math of this paper.

2.1 Noising and de-noising

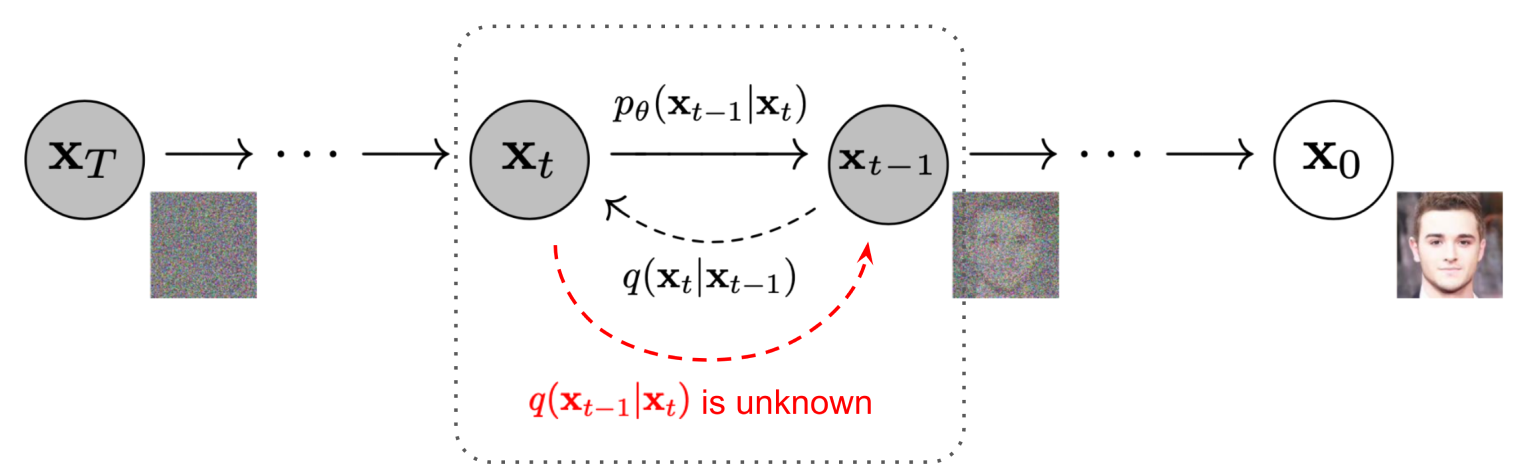
Given an input image \( \mathbf{x}_0 \), we map it to a point in the unit normal distribution by iteratively blending noise to it in a forward diffusion process over \(t=1,2,…,T\) timesteps. Each timestep generates a new image by blending in a small amount of random noise to the previous one: $$ \mathbf{x}_t = \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1-\alpha_t}\epsilon $$ where:

• \(\epsilon \sim \mathcal{N}(0, \mathbf{I})\)
• \(\alpha_t\) is less than but close to \(1\), and \(\prod_{t=1}^T \alpha_t \approx 0\)
• The terms in square roots ensure that the variance remains the same after each stepWe assume that the dataset is standardized, so that the variance of \(\mathbf{x}_0\) is 1 over all dimensions.. Notice how we are adding noise but shrinking the dataset at the same time.

We can write the probability density of the forward step as: $$ q(\mathbf{x}_t | \mathbf{x}_{t-1}) := \mathcal{N}(\sqrt{\alpha_t}\mathbf{x}_{t-1}, (1 - \alpha_t)\mathbf{I}) $$

Recurrence property

Each step depends only on the last timestep, and the noise blended in is independent of all previous noise samples. So we can expand the recurrence and derive an equation to obtain \(\mathbf{x}_t\) in one step from \(\mathbf{x}_0\) by blending in a single gaussian noise vector, since sums of independent gaussians are also gaussian: $$ \mathbf{x}_t = \sqrt{\bar\alpha_t}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon $$ where \(\bar\alpha_t = \prod_{i=1}^t \alpha_i\) and \(\epsilon \sim \mathcal{N}(0, \mathbf{I})\). This is used to derive the reverse process which we want to learn, and the training objective where we predict the noise that we add to images.

Image via .

Now consider the reverse process. Given a noisy image \( \mathbf{x}_t \), what's the distribution of the previous, less-noisy version of it \(q(\mathbf{x}_{t-1} | \mathbf{x}_t)\)?

This is easier if we know the original image \( \mathbf{x}_0 \). By Bayes' rule, we have: $$ q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \frac{q(\mathbf{x}_t | \mathbf{x}_{t-1}) q(\mathbf{x}_{t-1} | \mathbf{x}_0) q(\mathbf{x}_0)}{q(\mathbf{x}_t | \mathbf{x}_0) q(\mathbf{x}_0)} $$ Subbing in the distribution formulas and doing the algebra we get... $$ q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mu(\mathbf{x}_t, \mathbf{x}_0), \Sigma(t)\mathbf{I}) $$ where $$ \mathbf{\mu}(\mathbf{x}_t, \mathbf{x}_0) = \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})\mathbf{x}_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)\mathbf{x}_0}{1-\bar{\alpha}_t} \\ \Sigma(t) = \frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} $$ That is, given a noisy image and the known original image, the distribution of the previous, less-noisy version of it is gaussian.

What can we do with this information? When we're de-noising a noisy image we won't know the original corresponding to it. We want \( q(\mathbf{x}_{t-1} | \mathbf{x}_t) \).

Since we have a closed form solution for \(q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)\), if we could use the entire dataset at generation time, we could use the law of total probability to compute \(q(\mathbf{x}_{t-1} | \mathbf{x}_t)\) as a mixture of gaussians, but we can't (billions of images!) and moreover that would not give us the novelty we want, since if we followed it for all timesteps, we would just end up recovering the training samples. We want to learn some underlying distribution function which gives us novelty in generated samples by compressing the dataset.

2.2 Learning to de-noise

It turns out that \(q(\mathbf{x}_{t-1} | \mathbf{x}_t)\) is approximately gaussian for very small amounts of noise. This is an old result from statistical physics. This gives us a way to learn a reverse distribution: we can estimate the parameters \(\mu_\theta, \Sigma_\theta\) of a gaussian, and take the KL divergence to all of the distributions \(q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0)\) for every training example \(\mathbf{x}_0\).

Recall that the KL divergence is a metric measuring the difference between two probability distributions. It's easy to compute for us because we are computing it between two gaussians with known parameters, so it has a closed formFor arbitrary continuous distributions, the KL divergence requires taking an integral. This is a special case. See the formula and a short proof here.. And as it turns out, minimizing this gives us a distribution which is most likely to generate all our training samples.

The reverse distributions \(q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0^{(1)})\) and \(q(\mathbf{x}_{t-1} | \mathbf{x}_t, \mathbf{x}_0^{(2)})\) conditioned on training samples \(\mathbf{x}_0^{(1)},\mathbf{x}_0^{(2)}\), and the distribution \(p_\theta\) that we learn by minimizing KL divergence to them.

Concretely, let our training objective be: $$ L = \mathbb{E}_{\mathbf{x}_{0:T} \sim q}[\sum_{t=1}^TD_{KL}(q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) || p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t))] $$ where \(D_{KL}(q || p_\theta)\) is an expressionNote the KL divergence is asymmetric, so minimizing \(D_{KL}(q || p_\theta)\) over \(p_\theta\) (which squeezes \(q\) under \(p_\theta\)) gives a different result than \(D_{KL}(p_\theta || q)\) (which does the opposite). But as we see next this doesn't ultimately matter. involving the variances \(\Sigma_\theta,\Sigma(t)\) and means \(\mu_\theta,\mu(\mathbf{x}_t,\mathbf{x}_0)\) of the two gaussians.

Ho 2020 fixed the \(\Sigma_\theta\) to be equal to \(\Sigma(t)\), since they found that trying to learn it made training too unstable, and this gave good results. So in practice we only learn the means \(\mu_\theta\). After substituting in the KL divergence formula for gaussians, we end up with an objective to minimize the L2 distance between estimated and actual means: $$ L = \sum_{t=1}^T\mathbb{E}_{\mathbf{x}_{0:T} \sim q}[\frac{1}{2\Sigma(t)}||\mu(\mathbf{x}_t, \mathbf{x}_0) - \mu_\theta(\mathbf{x}_t)||^2] $$

We can simplify further and take advantage of the fact that \(\mathbf{x}_t\) can be written as a blending of \(\mathbf{x}_0\) with gaussian noise \(\epsilon\).

This means we can rewriteMuch thanks to Calvin Luo's blog for providing detailed derivations. I learned while writing this post that I like seeing detailed proofs only a little more than I dislike math. $$ \mathbf{\mu}(\mathbf{x}_t, \mathbf{x}_0) = \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}\epsilon $$ And we can define \(\mu_\theta(\mathbf{x}_t)\) in terms of an estimator \(\epsilon_\theta\) to match: $$ \mathbf{\mu}_\theta(\mathbf{x}_t) = \frac{1}{\sqrt{\alpha_t}}\mathbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}\sqrt{\alpha_t}}\epsilon_\theta(\mathbf{x}_t, t) $$

Plugging this in turns our mean prediction problem into a noise prediction problem: $$ L = \sum_{t=1}^T\mathbb{E}_{\mathbf{x}_{0} \sim q,\epsilon}[\frac{(1-\alpha_t)^2}{2\Sigma(t)\alpha_t(1-\bar{\alpha}_t)}||\epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon,t)||^2] $$

It turns out ignoring the weighting improves the quality of results. You could view this as down-weighting loss terms at small \(t\) so that the network focuses on learning the more difficult problem of denoising images with lots of noise. So the final loss function is $$ L_\text{simple} = \mathbb{E}_{t \sim [1, T], \mathbf{x}_{0} \sim q,\epsilon}[||\epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t}\mathbf{x}_0 + \sqrt{1-\bar\alpha_t}\epsilon,t)||^2] $$ In code, our training loop is:

            
def train(model, train_data, alpha_min=0.98, alpha_max=0.999, T=1000, n_epochs=5):
    opt = torch.optim.SGD([model.parameters()], lr=0.1)
    alpha = torch.linspace(alpha_max, alpha_min, T)
    alpha_bar = torch.cumprod(alpha, dim=-1)

    for _ in range(n_epochs):
        for x0s in train_data:
            eps = torch.randn_like(x0s)
            t = torch.randint(T, (x0s.shape[0],))

            xts = alpha_bar[t].sqrt() * x0s +  (1.-alpha_bar[t]).sqrt() * eps
            eps_pred = model(xts, t)

            loss = torch.nn.functional.mse_loss(eps_pred, eps)
            loss.backward()
            opt.step()
            opt.zero_grad()
            
        

2.3 Sampling

Once we've learned a noise estimation model \( \epsilon_\theta(\mathbf{x}_t, t) \), we've effectively learned the reverse process. Then we can use this learned model to sample an image \( \mathbf{x}_0 \) from the image distribution by:

1. Sampling a random noise image \(x_T \sim \mathcal{N}(0, \mathbf{I})\).

2. For timesteps \(t\) from \(T\) to \(1\):

   1. Predict the noise \(\hat\epsilon_t = \epsilon_\theta(\mathbf{x}_t, t)\).
   2. Sample the de-noised image \(\mathbf{x}_{t-1} \sim \mathcal{N}(\frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}}\hat\epsilon_t), \Sigma_\theta)\).

In code:

            
def sample(model, img_size, alpha, alpha_bar):
    xt = torch.randn(img_size)
    for t in reversed(range(T)):
        with torch.no_grad():
            eps_pred = model(xt, t)

        alpha_bar_t = alpha_bar[t]
        alpha_bar_t1 = alpha_bar[t-1] if t > 0 else 1.
        sigma = ((1.-alpha[t])*(1.-alpha_bar_t1)/(1.-alpha_bar_t)).sqrt()
        z = torch.randn(img_size)
        
        mu_pred = (xt - (1.-alpha[t])/(1.-alpha_bar[t]).sqrt()*eps_pred)/alpha[t].sqrt()
        xt = mu_pred + sigma*z
    return xt
            
        

2.4 Summary and example

Let's summarize what we've learned about DDPM:

• We want to learn an underlying distribution for a dataset of images.

• We do this by defining a forward noising process where we gradually turn an image \(\mathbf{x}_0\) into pure noise \(\mathbf{x}_T\) over many steps, and we learn to reverse the process by estimating the distribution of \(\mathbf{x}_{t-1}\) given \(\mathbf{x}_T\), which is feasible because:

  • It's approximately gaussian when \(T\) is large.
  • We know exactly what the distribution is if we assume the original image is some \(\mathbf{x}_0\) from our dataset.
  • We can use the KL divergence to ensure what we learn is as close to these known distributions as possible for every \(\mathbf{x}_0\) in our dataset.
  • This also provably maximizes the likelihood of re-generating our dataset.
• Finally, we can simplify the objective so it becomes a noise estimation problem.

Let's train a DDPM network on a 2D dataset. We will use the Datasaurus datasetInspired by tanelp's tiny-diffusion. of 142 points, plotted below. Follow along via Colab:

The neural network will be a function from \(\mathbb{R}^2 \mapsto \mathbb{R}^2\). We'll start with a bog-standard MLP with 3 hidden layers of size 64 with ReLU activations. This architecture has 12,000+ parameters, so one might think there is a high chance of memorizing the dataset (284 numbers), but as we'll see, the distribution we learn will be pretty good: it will not only fit the training samples but will have high diversity.

After training, we can sample 1000 points to see how well it learned the distribution:

Oh no! That doesn't look anything like the dinosaur we wanted. What happened?

One problem is that we're not passing any timestep information to the model. The noise drift vectors look pretty different at higher timesteps compared to lower timesteps. Let's try passing the timestep \(t=0,...,50\) normalized to between \(0\) and \(1\) to our model, which now map \(\mathbb{R}^3 \mapsto \mathbb{R}^2\).

That's much better. But we can do better by using input encodings. These are fixed functions that transform the input before feeding them to the neural network, and they can make a big difference. We will use a fourier encoding, since we know the distribution underlying our data is like an image - a high-frequency signal in a low-dimensional (2D) space.

For an input \(D\)-dimensional point \( \mathbf{x} \), we will encode it as: $$ \text{FourierEncoding}(\mathbf{x}) = \left[ \cos(2\pi\mathbf{Bx}), \sin(2\pi\mathbf{Bx}) \right]^T $$ here \(\mathbf{B}\) is a random \(L \times D\) Gaussian matrix, where each entry is drawn independently from a normal distribution. What we are doing is transforming the input space into a \(L\)-dimensional space of random frequency features. We'll set the hyperparameter \(L\) to 32.

Nice! Our distribution is looking pretty good. One more thing we can do is tweak our noising schedule. This can be crucial for performance.

• Our noising schedule is based on Ho 2020, who use a linearly decreasing sequence of \(\alpha_t\) where \(\bar\alpha_T=\prod_{t=1}^T\alpha_t\approx0\) so that the model spends a bit more time learning how to reverse lower noise levels, and the last timestep is close to pure noise. This works well for high-resolution images.
• But our dataset is low-dimensional, and from the forward process visualization in §1.1, it already looks a lot like noise once we get about halfway through our process, and subsequent steps don't seem to destroy much more signal.

Image via . The same amount of noise in different resolution images yields very different looking results, with low-res images looking much noisier than high-res ones.

Let's adjust our schedule so that the model trains on more high-signal examples. This improves performance on lower-dimensional data while doing the opposite for higher-dimensional data. It gets us our best dinosaur yet:

3.1 Faster generation

A major disadvantage of diffusion when it was first invented was the generation speed due to the DDPM assumption that the reverse distribution is gaussian, which is only true for large \(T\). Since then, many techniques to speed up generation have been developed, some of which can be used out-of-the-box on models pre-trained using the DDPM objective, while others require new models to be trained.

Score matching and faster samplers

Diffusion has a remarkable connection to differential equations, which enabled many faster samplers to be created as we were able to tap into the rich literature of the latter.

First, it turns out that the noise direction that we learn to estimate given a noisy input \(\mathbf{x}_t\) is equivalent For a proof, I like this video from Jia-Bin Huang or blog post from Calvin Luo. to the gradient of the log-likelihood of the forward process generating \(\mathbf{x}_t\) (also known as the score of \(\mathbf{x}_t\)) up to a constant which depends on timestep: $$ \nabla_{\mathbf{x}_t} \log q(\mathbf{x}_t) = -\frac{1}{\sqrt{1-\bar\alpha_t}}\hat\epsilon_\theta(\mathbf{x}_t, t) $$ This is interesting by itself. To see why, ignore the forward process for a second and assume that we have learned the score for \(\mathbf{x}_0\). If we imagine that \(\mathbf{x}_0\) has nonzero probability everywhere in image space, then the score would provide a vector field over the entire space that would tell us in what direction we should walk if we want to move towards the modes of the distribution. But in real life \(\mathbf{x}_0\) does not have nonzero probability everywhere. If we add noise to it, we can spread density out to where there is none, but keep the modes the same.

From Calvin Luo's blog: Sampling by following the score function in a mixture of gaussians. These sampling trajectories all start from the center and have noise injected at each step. In the context of DDPMs, the noise is needed to model the reverse distribution correctly, while in the context of score-based models, the noise is needed to avoid having sampling just converge on a mode.

This formed the basis for noise-conditioning score networks, which learned the score of a progressively noised dataset and generated new samples by iteratively following the score field. If that sounds familiar, that's because it is basically the same as diffusion!

Second, it turns out that the forward diffusion process can be described by something called a stochastic differential equation (SDE) which tells us how the data distribution evolves over time as we add noise to it. And here is the magic part: there exists an ODE that describes a deterministic process whose time-dependent distributions are exactly the same as the stochastic process at each timestep, with a simple closed form involving the score function from aboveSee this introduction from Eric Ma for details.!

Comparison of reverse SDE and ODE trajectories in a diffusion of a 1-dimensional dataset. The x-axis represents the timestep \(t\), while the y-axis represents the value of \(\mathbf{x}_t\). The color is the probability density of that value at that timestep. Notice how much straighter the ODE trajectory is, which suggests a way to "speed" sampling by stepping in larger increments.

Not only does this mean that there exists a fully deterministicE.g. without injecting noise way to sample from any given pretrained diffusion model, but it also means we can use off-the-shelf ODE solvers to do the sampling for us. Whereas DDPM can take up to 1000 steps to sample a high-quality result in Stable Diffusion, a sampler based on the Euler method of solving ODEs can yield high quality results in as little as 10 steps. Karras 2022 (video) provide a great overview of the tradeoffs of these and how stochasticity of samplers like DDPM can still be important in some cases.

3.2 Conditional generation

Given a model trained on animal images, how do I generate only cats?

In principle, it's possible to model any type of conditional probability distribution \(p(\mathbf{x} | y)\) by training a diffusion model \(\epsilon_\theta(\mathbf{x}_t, t, y)\) with pairs \(\mathbf{x}_0, y\) from the dataset. This was done by Ho 2021, who trained a class-conditional diffusion model on ImageNet. The label \(y\) can also be a text embedding, a segmentation mask, or any other conditioning information.

Class-conditional generations for ImageNet from .

However, the label can sometimes lead to samples that are not realistic or lack diversity if the model has not seen enough samples from \(p(\mathbf{x} | y)\) for a particular \(y\). So we often want to tune how much the model “follows” the label during generation. This leads to the concept of guidance.

Classifier guidance

Given an image \(\mathbf{x}_0\), a classifier gives a probability distribution \(p_\phi(y|\mathbf{x}_0)\) that it lies in some class \(y\). If we take the gradient of that with respect to the input, we get a vector \(\nabla_{\mathbf{x}_0}p_\phi(y|\mathbf{x}_0)\) which we can use to push the image This is similar to how Google's DeepDream worked back in the day. towards our class \(y\).

What if each sampling step, we added the classifier gradient with respect to \(\mathbf{x}_t\) to our estimated mean? Hopefully, the diffusion will ensure the sample will land in some plausible region of image space. To ensure our classifier knows what to do with the (potentially very noisy) image \(\mathbf{x}_t\), we'll train it on noisy images.

This turns out really well experimentally and mathematically. For DDPM, if we set our reverse step estimated mean to $$ \mu_{\theta,\phi}=\mu_\theta + \sigma_t^2 * \nabla_{\mathbf{x}_t}\log p_\phi(y | \mathbf{x}_t)|_{\mathbf{x}_t=\mu_\theta} $$ Then it can be shown to a first order approximation that we're sampling from the distribution $$ p_{\theta,\phi}(\mathbf{x}_{t}|\mathbf{x}_{t+1}, y) \propto p_\theta(\mathbf{x}_{t}|\mathbf{x}_{t+1})p_\phi(y|\mathbf{x}_t) $$

The classifier used doesn't need to be particularly high-quality. For example, here are classifier-guided examples for the "T-shirt" class on Fashion-MNIST using a classifier with 40% accuracy:

The level of guidance parameter cg scales the classifier gradient. More guidance leads to stronger class characteristics but possibly less realism.

Classifier-free guidance

Training a classifier takes extra work. Can we do guidance without one? Let's apply Bayes' rule to our class gradient: $$ \nabla_{\mathbf{x}_t}\log p(y | \mathbf{x}_t) = \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t | y) - \nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t) $$ We have turned our class gradient into two score (§3.1) functions:

1. \(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t | y)\) is the score of the data \(\mathbf{x}_t\) conditioned on class \(y\).
2. \(\nabla_{\mathbf{x}_t}\log p(\mathbf{x}_t)\) is the score of all the data \(\mathbf{x}_t\).

We have seen that denoising diffusion models learn the score of their training data, so this gives us an approach for guidance without a classifier:

1. Train a single diffusion model on every training sample \(\mathbf{x}_0\) twice: once paired with its class label \(y\), and once paired with a null class label.
2. When sampling from the model, call it twice: once with the desired class label and once without, then take the difference and use that as our guidance vector.

Image conditioning

Image-to-image

Image-to-image doesn't require retraining a model. Instead, given an input image, we can add noise to the image according to the desired strength of the conditioning image (less noise for stronger conditioning), then de-noise it.

Inpainting

Inpainting is filling in a masked part of an image. One idea to implement this would be via image-to-image: rather than adding noise to the whole image, we just add it to the masked part. But this doesn't work because at any \(t > 0\), the denoising model doesn't know what to do with the non-noisy parts of the image.

Image via .

Instead, what works is to add noise to both the masked and un-masked parts of the image, and pass that in as \(\mathbf{x}_T\). Then at each subsequent sampling step \(t\), given \(\mathbf{x}_t\), we copy the un-masked parts of the original image, noise them according to \(t\), then place them over \(\mathbf{x}_t\) and use that as input into the denoiser.

Text-to-image

Imagen at a high-level.

Text-to-image is conditional generation with text embedding labels. OpenAI's Dall-E trained an encoding model called CLIP to project both images and text into the same space, but a multimodal embedding space is not strictly required. Google's Imagen model used the T5 large language model to encode text into embeddings. As long as the embeddings are a rich enough representation, any can be used.

3.3 Data

While not specific to diffusion, no discussion of generative models is complete without mentioning the data they were trained on. This section will cover data used for image generation models.

Searching for 'cat' in LAION.

Searching for 'cat' in LAION-aesthetic.

• Dall-E 1 was trained on 250 million text-image pairs, and Dall-E 2 was trained on 650 million. The dataset is closed source.
• According to the HuggingFace model card, Stable Diffusion 1 was trained on LAION-2B-en (2 billion pairs), then fine-tuned on 170 million pairs from LAION-5B.
• Subsequent checkpoints of Stable Diffusion 1 are fine-tuned on subsets of LAION-5B selected for “aesthetics”From the LAION-aesthetic readme, as automatically labeled by a linear regression on CLIP trained on 4000 hand-labelled examples.. See this blog post for a look inside.
• LAION itself is derived from the Common Crawl. LAION-400M was released in August 2021 and was an attempt to recreate the process used by OpenAI to train the CLIP model. The developers collected all HTML image tags that had alt-text attributes, and treated the latter as the image captions, using CLIP to discard those which did not appear to match their content.
• Some users have also compiled lists of artists that appear in LAION. For example see MisterRuffian's Latent Artist Encyclopedia. The website haveibeentrained.com also allows users to check if their images are in LAION or other popular datasets.

A major component of the AI art backlash is the ethics of collecting art for datasets like LAION and training image generation models on them without the consent of the artists, especially since image models can pose a direct threat to the livelihoods of those artists. However, there have been efforts to train competitive image generation models more ethicallySimon Willison calls these "vegan" models.. For example, Adobe Firefly is supposed toExcept for a recent scandal where Firefly was trained on some Midjourney images. be trained only on licensed content, such as Adobe Stock, and public domain content where copyright has expired. Additionally, Stable Diffusion 3 allowed artists to opt-out of having their images be used for training, with over 80 million images removed as a result.

Data poisoning

Nightshade is an example of a data poisoning attack against image generation models which received attention during the AI art backlash. Models are trained on billions of images, but for a given concept there might only be dozens. The idea of Nightshade is to poison data on a concept-specific basis.

The authors demonstrate an attack against Stable Diffusion XL using 50 images modified to cause the model to output a cow for every mention of “car” in its prompts. The modification is engineered to be as un-noticeable to the human eye as possible, by optimizing a multi-objective function involving perceptual loss.

An initial attack requires access to a model's feature extractor. The authors then examine how an attack based on 1 of 4 models performs on all the others, and say the results show their attack will generalize to models besides the initial model.

4.1 Audio, video, and 3D

Riffusion was an early music generation model capable of generating twelve-second long songs, notable because it was made by fine-tuning Stable Diffusion to output spectrogram images. Sonauto is a more recent and controllable model built on diffusion transformers, capable of generating 1:35-long songs with coherent lyrics.

From left to right: scaling compute 1x, 4x, and 32x with Sora.

OpenAI's Sora and Google's Veo are diffusion transformer video generation models capable of generating minute-long 1080p video clips from text prompts. At a high level, Sora works by decomposing videos into spacetime patches, then learning to denoise patches.

A key insight of the Sora technical report is that diffusion transformers scale for video generation, and that performance scales with computeOpenAI did not clarify what "compute" means in this context (dataset size, model size, or training time).. Both models support various video editing tasks such as masked editing, creating perfectly looping video, animating static images, extending videos forwards or backwards in time, etc. They build on past video diffusion work like Imagen Video (2022). Autoregressive models like VideoPoet (2024) are an alternative to diffusion in this space.

One remarkable aspect of 2D diffusion models is that they implicitly learn some 3D features like correspondences. DreamFusion (2022) exploited this to generate 3D models from text by using a text-to-image diffusion model as a prior to guide a gradient-descent based 3D reconstruction algorithmThey propose something called Score Distillation Sampling to allow the image model to provide a loss for a differentiable renderer. Surprisingly, dumber techniques like generating multiple views by clever prompting of the text-to-image model can also yield decent, though lower-quality outputs.. Stable Video 3D (2024) is a more recent work which uses video diffusion for improved multi-view consistency. Such models still rely on 3D reconstruction algorithms like photogrammetry, 3D gaussian splatting, or neural radiance fields to generate the 3D representation, possibly due to the relative sparsity of 3D dataFrom Twitter, 3D artists have learned from 2D artists how important ownership of their data is, so if this is going to change, it must do so in a more creator-friendly way..

4.2 Life sciences

Diffusion models are finding many applications in medicine and biology. For example, performing partial CT and MRI scans greatly reduces patient exposure to radiation and increases comfort, but is challenging because it requires reconstructing full scans from partial data. Diffusion models have advanced the state-of-the-art in medical image reconstruction, providing superior performance and generalization to supervised methods.