Python is the most popular programming language in the world. It is an extremely simple and accessible language, making it the go-to choice for developers across numerous domains. It is used in everything from introduction to computer science classes; to powering the AI revolution we're all living through.

However, Python's convenience comes with two significant drawbacks: First, running an interpreted language results in much slower execution compared to native languages like C or Rust. Second, it is incredibly difficult to embed Python-powered functions (e.g. Numpy, PyTorch) into cross-platform consumer applications (e.g. web apps, mobile).

But what if we could compile Python into raw native code?

Compiling a Toy Function

Artificial Intelligence, and particularly Large Language Models (LLMs), rely heavily on matrix multiplications. These matrix operations, at their core, utilize a fundamental operation known as fused multiply-add (FMA):

def fma (x, y, z):
    """
    Perform a fused multiply-add.
    """
    return x * y + z

Hardware vendors like Nvidia provide specialized instructions that perform the FMA in a single step, reducing computational overhead and improving numerical precision. Given that LLMs perform billions of these operations, even minor performance variations can significantly affect overall efficiency.

result = fma(x=3, y=-1, z=2)
print(result)
# -1

Let's explore how to compile the fma function, allowing it to run at native speed, cross-platform.

Tracing the Function

We begin by capturing all operations performed within the function as a computation graph. We call this an Intermediate Representation (IR). This IR graph explicitly represents every operation—arithmetic operations, method calls, and data accesses—making it a powerful abstraction for compilation.

To build this graph, we leverage CPython's frame evaluation API to perform Symbolic Tracing. This allows us to introspect Python bytecode execution, capturing each instruction's inputs, operations, and outputs dynamically as the function executes. By tracing each Python operation in real-time, we construct an accurate IR of the function’s logic. For example:

from torch._dynamo.eval_frame import set_eval_frame

# Define a tracer
class Tracer:

    def __call__ (self, frame, _):
        print(frame.f_code, frame.f_func, frame.f_locals)

# Set the frame evaluation handler
tracer = Tracer()
set_eval_frame(tracer)

# Call the function
result = fma(x=3, y=-1, z=2)
print(result)
# <code object fma at 0x106c51ca0, file "fma.py", line 9> <function fma at 0x106ba4860> {'x': 3, 'y': -1, 'z': 2}
# -1

Skipping a few steps ahead, we end up with a graph that looks like this:

type           name       target        args
-------------- ---------- ------------- --------
input          x          x             ()
input          y          y             ()
input          z          z             ()
call_function  mul_result _operator.mul (x, y)
call_function  add_result _operator.add (mul_result, z)
output         output     output        (add_result,)

An astute reader might notice that in order to build the IR graph above, we need to actually invoke the fma function. And to do that, we need to pass in inputs with the correct types to the function. We can simply add type annotations to our fma function, and generate fake inputs to invoke the function:

def fma (x: float, y: float, z: float) -> float:
    """
    Perform a fused multiply-add.
    """
    return x * y + z

Lowering to Native Code

Now the real fun begins! With our IR graph and annotated input types, we start the process of lowering the IR graph into native code. Let's take the first operation in the graph, x * y:

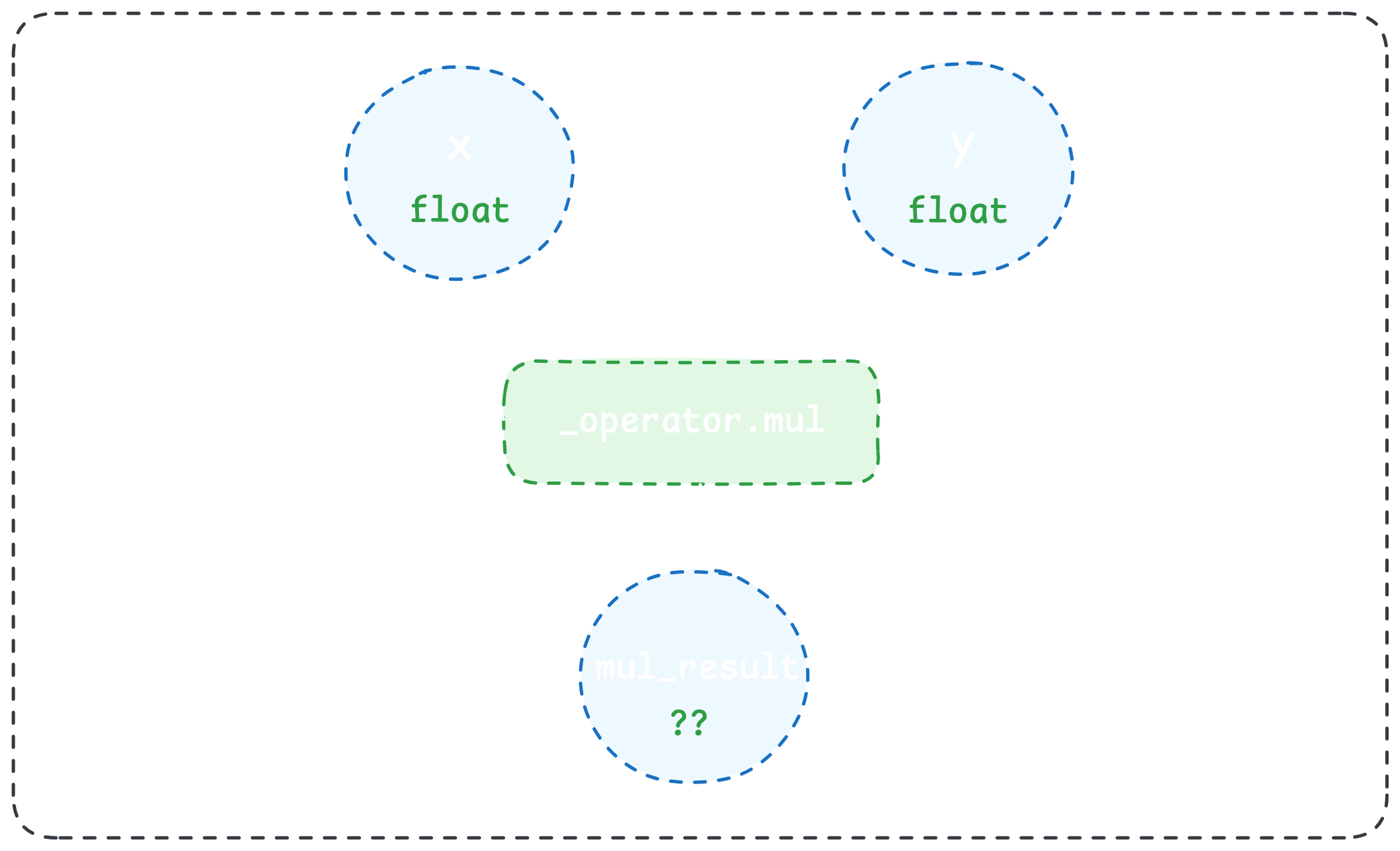
We can write (*ahem* generate) a corresponding implementation of the _operator.mul operation in native code. For example, here's a C implementation:

float _operator_mul (float x, float y) {
    return x * y;
}

Notice that because of the return type of the native implementation above, the type of mul_result is now constrained to be a float. Zooming out, this means that given inputs with known types (i.e. from type annotations in Python) along with a native implementation of a Python operation, we can fully determine the native type of the operation's outputs. By repeating this process to subsequent operations in our IR graph, we can propagate native types through our entire Python function:

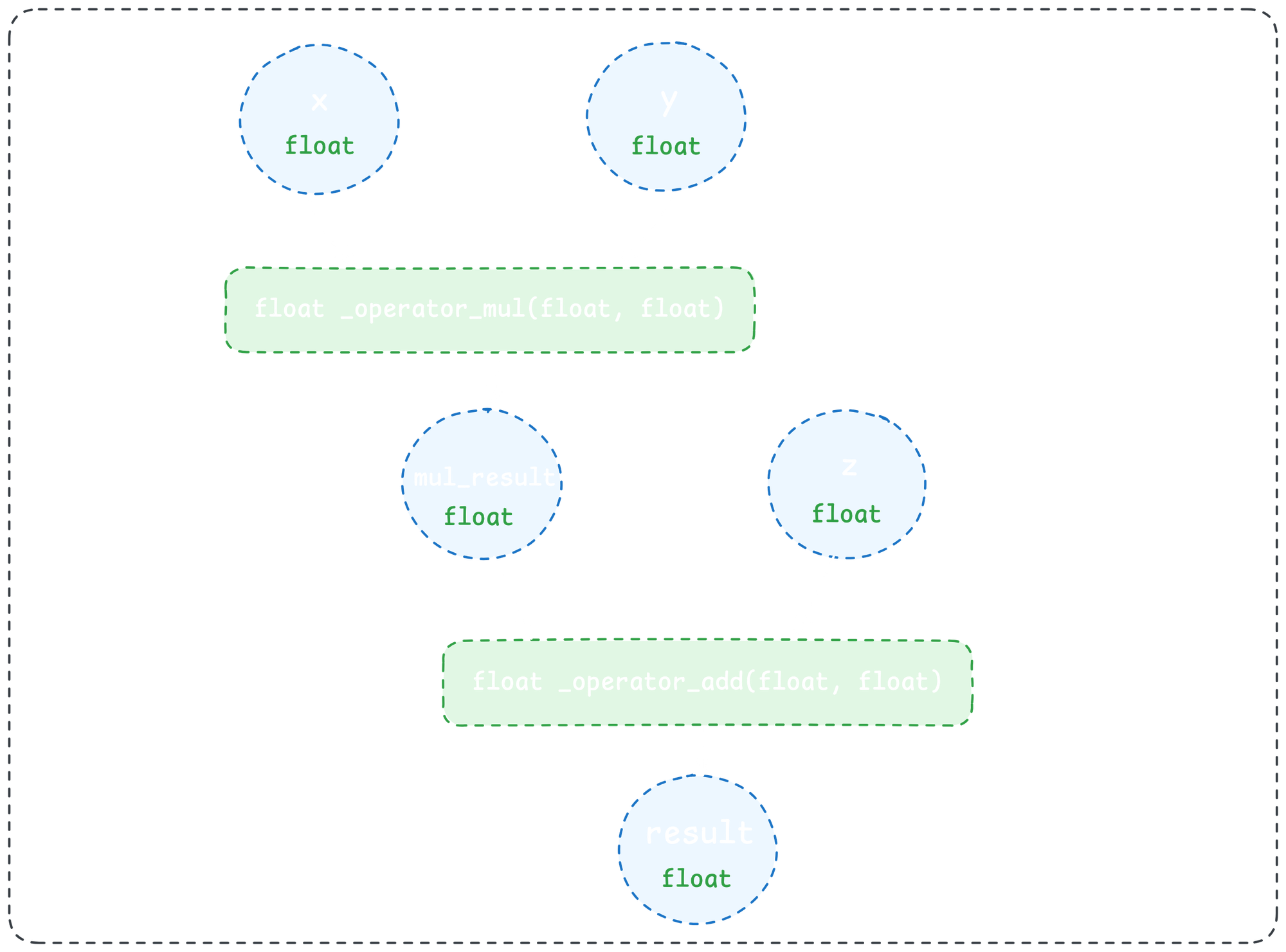
We can now cross-compile this native implementation for any platform we want (WebAssembly, Linux, Android, and much more). And that's how we get Python to run as fast as Rust—and run everywhere!

Compiling the Function

Let's use Function to compile the fma function based on the above process. First, install Function for Python:

# Run this in Terminal
$ pip install --upgrade fxn

Next, decorate the fma function with @compile:

from fxn import compile

@compile(
    tag="@yusuf/fma",
    description="Fused multiply-add."
)
def fma (x: float, y: float, z: float) -> float:
    """
    Perform a fused multiply-add.
    """
    return x * y + z

Finally, compile the function using the Function CLI:

# Run this in terminal
$ fxn compile fma.py

Let's Benchmark!

First, let's modify our fma function to perform the fused multiply-add repeatedly:

def fma (x: float, y: float, z: float, n_iter: int) -> float:
    for _ in range(n_iter):
        result = x * y + z
    return result

Next, we'll create an equivalent implementation in Rust:

use std::os::raw::c_int;

#[no_mangle]
pub extern "C" fn fma (x: f32, y: f32, z: f32, n_iter: c_int) -> f32 {
    let mut result = 0.0;
    for _ in 0..n_iter {
        result = x * y + z;
    }
    result
}

After compiling both, here's a graph of the performance on my MacBook Pro:

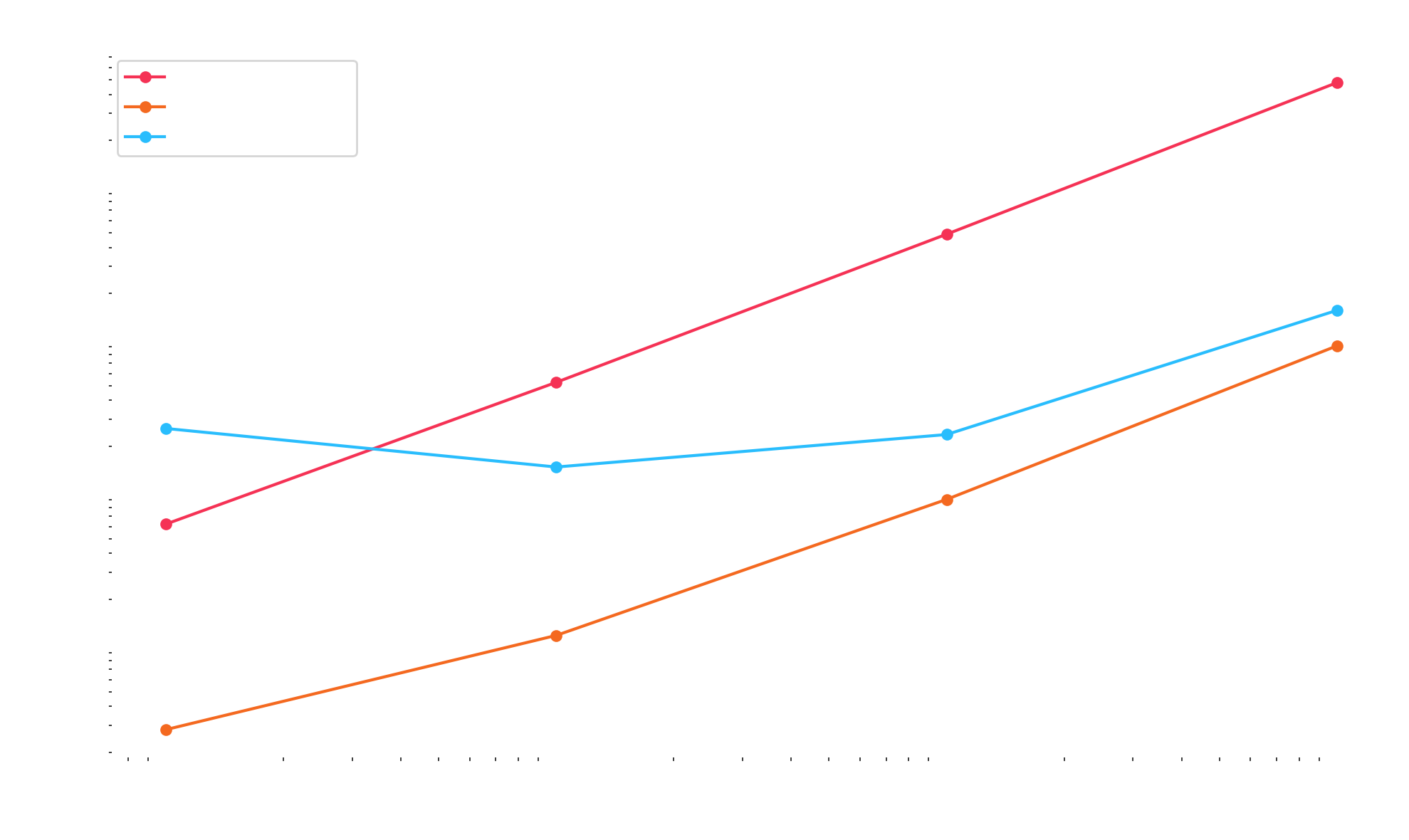
The compiled Python benchmark is slower than Rust by a constant factor because Function has extra scaffolding to invoke a prediction function, whereas the Rust implementation uses a direct call. You can inspect the generated native code and reproduce the benchmark with this repository:

Wrapping Up

The prospect of being able to compile Python is very exciting to us. It means that we can accelerate scientific computing, realtime data processing, and AI workloads to run on many more devices—all from the convenience of Python.

Our compiler is still a proof-of-concept, but with it our design partners have been shipping applications into production, powering everything from monocular depth estimation to realtime pose detection. Up next? On-device LLM inference. Join the conversation: