The younger child and I were talking about maths on the school run this morning, and today’s topic was geometry. I was pleased to discover that he’s already got a reasonable comprehension of the Pythagorean Theorem: I was telling him that I was about his age when I first came across it, but in my case I first had a practical, rather than theoretical, impetus to learn it.
It was the 1980s, and I was teaching myself Dr. Logo, Digital Research‘s implementation of the Logo programming language (possibly from this book). One day, I was writing a program to draw an indoor scene, including a window through which a mountain would be visible. My aim was to produce something like this:
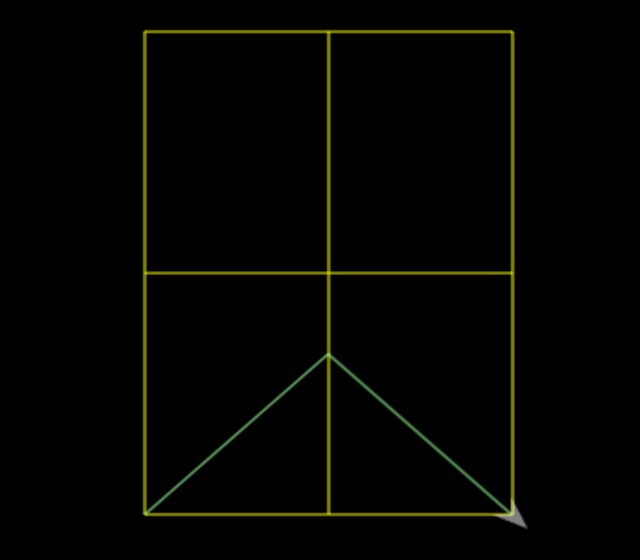
My window was 300 “steps” tall by 200 steps wide and bisected in both directions when I came to make my first attempt at the mountain.
And so, naively, starting from the lower-left, I thought I’d need some code like this:
RIGHT 45 FORWARD 100 RIGHT 90 FORWARD 100
But what I ended up with was this:
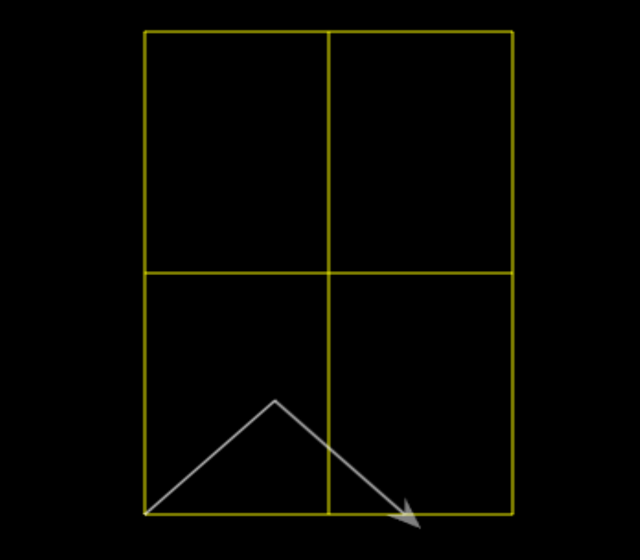
I instantly realised my mistake: of course the sides of the mountain would need to be longer so that the peak would reach the mid-point of the window and the far side would hit its far corner. But how much longer ought it to be.
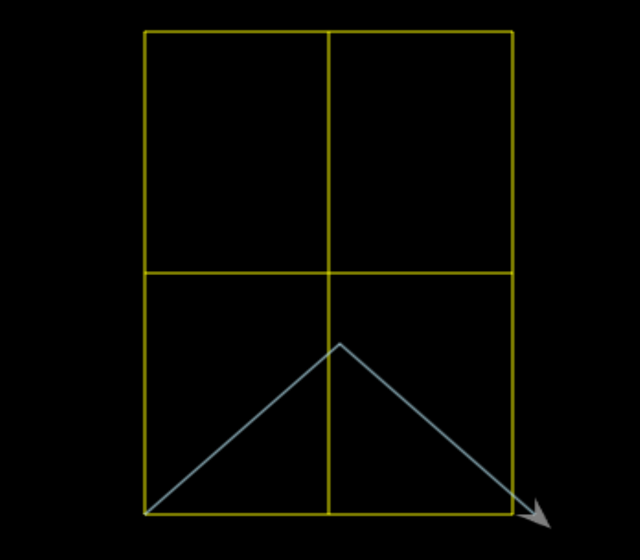
I intuited that the number I’d be looking for must be greater than 100 but less than 250: these were, logically, the bounds I was working within. 100 would be correct if my line were horizontal (a “flat” mountain?), and 250 was long enough to go the “long way” to the centrepoint of the window (100 along, and 150 up). So I took a guess at 150 and… it was pretty close… but still wrong:
So I found my mother and asked her what I was doing wrong. I’m sure it must have delighted her to dust-off some rarely-accessed knowledge from her own school years and teach me about Pythagoras’!
The correct answer, of course, is given by:
The answer, therefore, is… 141.421 (to three decimal places). So I rounded to 141 and my diagram worked!
What made this maths lesson from my mother so memorable was that it fed a tangible goal. I had something I wanted to achieve, and I learned the maths that I needed to get there. And now it’s impermeably etched onto my brain.
I learned the quadratic equation formula and how to perform algebraic integration by rote, and I guarantee that it’s less well-established in my long-term memory than, say, the sine and cosine rules or how to solve a simultaneous equation because I’ve more-often needed to do those things outside of the classroom!
So I guess the lesson is that I should be trying to keep an eye out for practical applications of maths that I can share with my kids. Real problems that are interesting to solve, to help build the memorable grounding that latter supports the more-challenging and intangible abstract maths that they may wish to pursue later.
Both kids are sharp young mathematicians, and the younger one seems especially to enjoy it, so feeding that passion feels well-worthwhile. Perhaps I should show them TRRTL.COM so they can try their hand at Logo!