In this post: why I expect the maximum achievable qubit quality to increase drastically in the next few years.

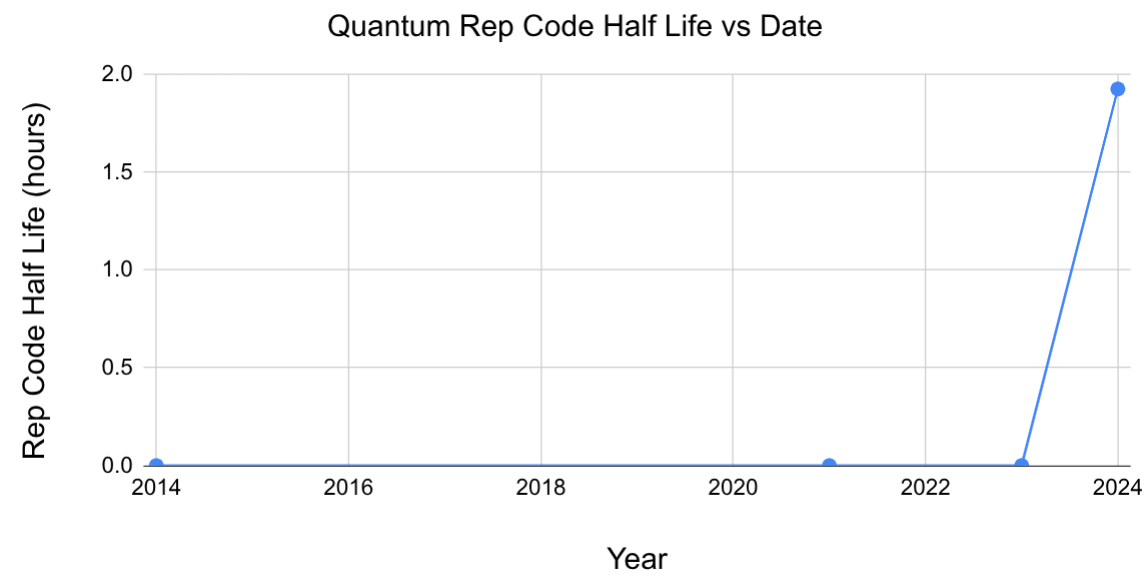
In 2014, the John Martinis group at UCSB performed an experiment where they stored a classical bit using their quantum computer. They protected the bit with a 9 qubit quantum repetition code. The protected bit had a half life of roughly 100 microseconds. Clearly that’s not competitive with classical storage… but the goal of the experiment wasn’t to hit a high number. The goal was to perform a demonstration of the fledgling power of quantum error correction. In particular, the 9 qubit rep code had a longer lifetime than the individual physical qubits, and also a longer lifetime than the 5 qubit rep code that they also tried. It hinted that qubit quality could be solved using qubit quantity.

Later experiments by the same group (now at Google) improved on this starting point. In 2021, it was a 21 qubit rep code with a half life of 3 milliseconds. Then, in 2023, it was a 51 qubit rep code with a half life of 300 milliseconds. Most recently, in 2024, it was a 59 qubit rep code with a half life of 2 hours.

Let’s plot this data:

(view with semilog scale instead)

That’s quite the plot, right? There’s a huge lull and then… FOOM! It took nearly a decade for the half life to approach one second, and then one year later it’s suddenly measured in hours?! I know why it happens, but I still find it surprising.

Here’s a simple model that explains the FOOM. The lifetime $L$ of a repetition code grows like $L = C \lambda^q$ (see equation 11 of “Surface codes: Towards practical large-scale quantum computation”). Here $q$ is the number of physical qubits, $\lambda$ is a measure of qubit quality, and $C$ is a starting constant. Suppose quality is held fixed at $\lambda = 2$ and qubit count doubles each year (meaning $q = 2^t$). Then $L$ grows superexponentially:

The first stacked exponential is qubit count vs years, due to the assumed Moore’s-law-like growth. The second stacked exponential is error rate vs qubit count, due to technical details of how quantum error correction works that I’m not going to go into.

What do you get when you stack two exponentials? A lull followed by a FOOM.

In practice, things are a bit more complex than a superexponential. There are “hurdles” that place ceilings on the lifetime of error corrected objects. You discover these QEC hurdles due to the superexponential not holding, and you get mini FOOMs as you fix them. A mundane example of a QEC hurdle is, if you don’t have backup generators, your qubits can’t live longer than the time between power outages. Installing backup generators would allow the lifetime to increase, until it becomes limited by whatever the next QEC hurdle is (such as asteroid strikes).

An important QEC hurdle is leakage. During operation, superconducting transmons can get overexcited and “leak” out of the qubit subspace. The proportion of leaked qubits will grow until they suffocate the computation. Fixing this requires some kind of leakage removal. Another important QEC hurdle is high energy events like cosmic rays. The 2023 lifetime of 300 milliseconds noticeably deviated from the $L = C \lambda^q$ idealization, due to high energy impacts intermittently disabling the entire chip. In 2024 this problem was mitigated using gap engineering, resulting in the sudden 10000x jump in lifetime. Without cosmic rays (or other QEC hurdles), the lifetime would have already been unmeasurably long in 2023.

QEC hurdles are extremely important to identify and fix. In fact, this is one of the major reasons the google team does rep code experiments. To clear the way for full quantum error correction.

So far I’ve only talked about protecting a classical bit on a quantum chip. That only requires correcting one type of error (bit flip errors). The real goal is, of course, to protect quantum bits. Protecting a qubit requires correcting a second type of error (phase flip errors, such as caused by unwanted measurements). Repetition codes protect against bit flips, but actually make phase flip errors worse. Correcting both simultaneously requires more complex codes, such as the surface code.

Although the process of protecting a qubit is more complex than protecting a bit, the same basic dynamics are present. There’s a quality bar you must cross in order for it to work, and then you get exponential returns on error suppression by increasing qubit count. If your qubit count is also increasing exponentially, then you will achieve superexponential error suppression vs time (with ceilings as you encounter QEC hurdles).

In a surface code, quadrupling the number of physical qubits will square the logical error rate of the protected qubit. In 2024, the best surface code experiment had a logical error rate of 0.1% per round (corresponding to a half life of a ~300 microseconds). Holding quality constant, one qubit quadrupling would turn that 0.1% into 0.0001% (~300 milliseconds). The next quadrupling would reach 0.0000000001% (~3 days). And the one after that would reach 0.0000000000000000000001% (~30 billion years).

Quadrupling the number of physical qubits has technical challenges, like wiring complexity, which must be overcome in a way that doesn’t degrade qubit quality. And, of course, there will be some QEC hurdle that places a ceiling stricter than 30 billion years (e.g. nuclear war). But ultimately the picture looks qualitatively similar to the rep code case. Lull… then FOOM.

Because error corrected qubits recently begun to surpass physical qubits, I think the FOOM for logical qubits is near. I realize how ridiculous the hypotheticals look in this plot, but I legitimately think this is what will happen:

In my view, there are three long standing barriers to full scale quantum computation: qubit quality, qubit quantity, and qubit speed. I think the quality barrier will fall within the next five years. This is perhaps surprising, because the quality barrier has held strong over the three decades that we’ve known about quantum error correction. But logical qubits have recently begun surpassing physical qubits, and QEC goes FOOM.