韩国81998家酒吧的最短步行路线——旅行商问题在178天内解决

韩国81998家酒吧的最短步行路线——旅行商问题在178天内解决
Shortest-possible walking tour to 81,998 bars in South Korea

原始链接: https://www.math.uwaterloo.ca/tsp/korea/index.html

研究人员解决了韩国一个包含81,998个节点的旅行商问题（TSP），这是迄今为止已证明最优解的规模最大的道路地图TSP实例。这条史诗般的“酒吧之旅”估计步行时间为15,386,177秒（约178天），使用了开放源代码路由机（OSRM）生成的点对点旅行时间。该解决方案超过了此前荷兰57,912个节点的TSP记录，展示了将LKH代码用于近似最优路径与Concorde的切割平面法用于验证相结合的强大力量。这种方法克服了检查所有可能路径的计算挑战，突显了高效算法可以解决看似不可能的问题。该项目强调了数学优化在高效资源分配中的重要性，其应用遍及各个行业。交互式地图和高分辨率的路线快照可在网上访问，使用户能够详细探索该解决方案。研究使用了IBM CPLEX优化器、Leaflet、OpenStreetMap、Carto底图和Stadia地图。数据来源包括韩国国家警察厅和OSRM。

一个Hacker News帖子讨论了滑铁卢大学的一个项目，该项目找到了韩国81998家酒吧的最短步行路线，这是一个复杂的旅行商问题（TSP）。用户们就这条路线的可行性展开了辩论，考虑了酒吧倒闭、恒星运动（参考团队针对13.3亿颗恒星的类似TSP解决方案）甚至时间相对性等因素。一些用户质疑城市停车最低限额的实用性。讨论还延伸到所使用的算法，特别是Lin-Kernighan启发式算法（LKH）和2-opt算法。一些评论者对韩国酒吧数量之多感到惊讶，并将其与俄亥俄州和纽约州等其他地区进行了比较，一些人认为该数据集可能是韩国任何拥有酒类销售许可证场所的过于广泛的列表。一位用户询问但未找到关于算法最优性“证明”的清晰易懂的解释，尽管提到了运行时执行日志。

货船数学优化 2024-06-07

研究人员找到了一种更快的整数线性规划方法 2024-01-31

动漫迷偶然发现了一个数学证明 2025-03-08

苏黎世联邦理工学院的研究人员开发出最快的流程算法 2024-07-01

原文

We have solved a traveling salesman problem (TSP) to walk to 81,998 bars in South Korea. The problem was created using the Open Source Routing Machine (OSRM) to build a table of the 3,361,795,003 point-to-point travel times, one for each pair of bar locations. Our computation produced a tour together with a proof that it is a shortest-possible route to visit all 81,998 stops when measured with the OSRM times.

It would be a very long pub crawl. The total walking time for the round trip is 15,386,177 seconds, or 178 days, 1 hour, 56 minutes, and 17 seconds. You will need to stop for plenty of drinks along the way (better stick with water, tea, or Diet Coke if you want to finish the route in only a few years), so it's not likely you would count every second on such a journey. But the level of precision makes the point that this not just a good route, it is an optimal solution to the 81,998-stop TSP. It is not possible to rearrange the order of stops to save even a single second of the OSRM-estimated walking time.

This is the largest road-map instance of the TSP that has been solved to provable optimality, exceeding the 57,912-stop tour through the Netherlands solved in February 2021. The computations were carried out between December 2024 and March 2025 at Roskilde University and at the University of Waterloo. Details of the computing work can be found on the Computation page.

Interactive map

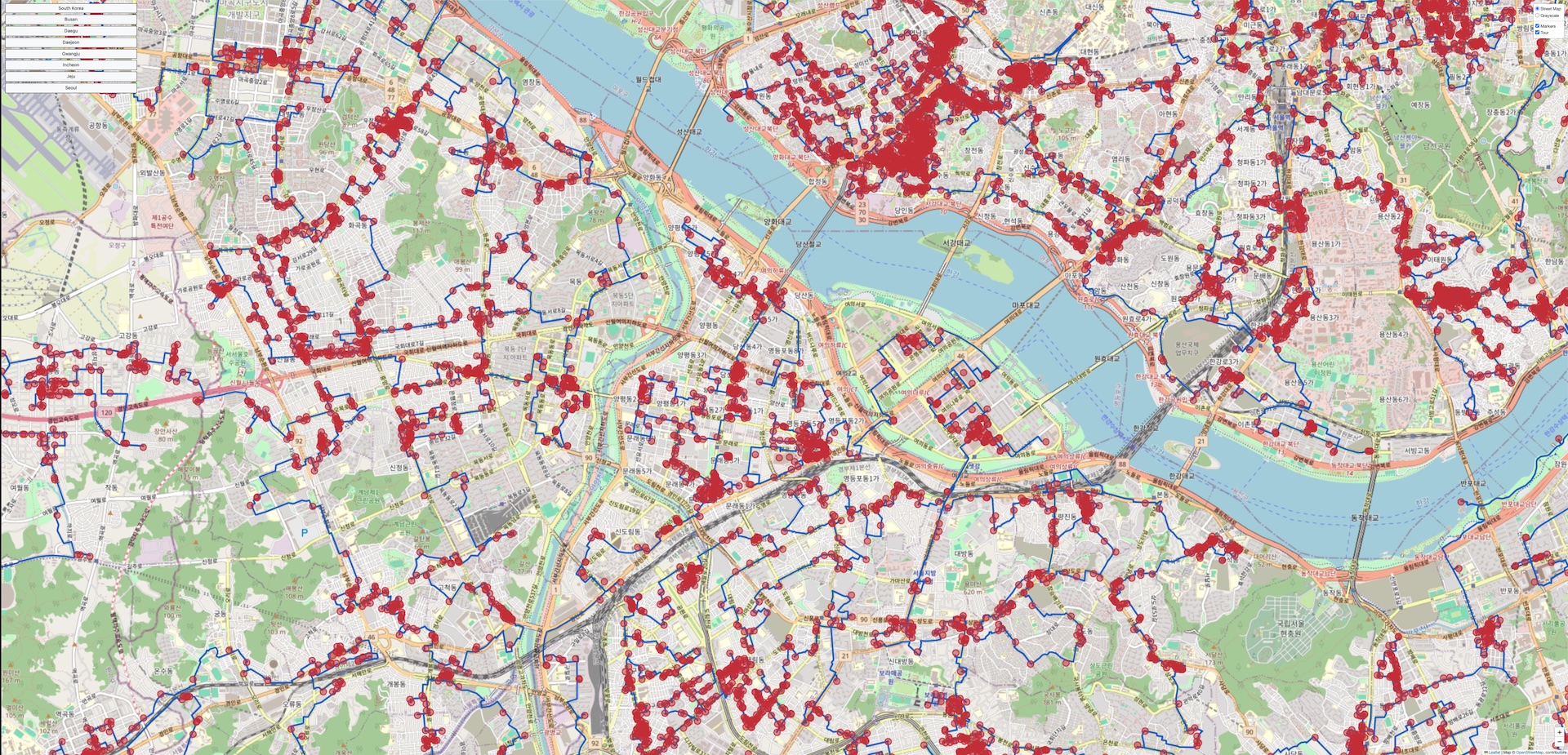
The figure below is a screen shot of an interactive map of the korea81998 tour. The menu on the left-hand-side lets you select one of seven regions to view. At the top right-hand-side you can choose to have either a colored street map or a grayscale map without street labels. Just below this menu you can select whether or not to display the stop markers, or to display the tour edges, or to display both. You can view the map by clicking on the image.

Snapshots of the Tour

If you have trouble viewing the interactive map, you can click on the drawings below to see high-resolution images of the tour. For close-up views of city regions, please see the Cities page.

Optimality

Newspapers, popular journals, blogs, and scientific press releases regularly report that solving even tiny instances of the TSP is impossible with the current generation of computers. A typical example is the following quote from the Washington Post.

"It would take a laptop computer 1,000 years to compute the most efficient route between 22 cities, for example."

Statements such as this assume the only way to solve the TSP is to check each possible tour, one-by-one. That clearly cannot work for any of the large instances of the TSP we have solved. The number of tours in the korea81998 case is roughly 2 followed by 367308 zeroes.

This huge number of possible solutions is frightening, but it doesn't mean we can't solve this large example of the TSP. Our approach combines the LKH code for computing extremely good TSP solutions and the Concorde code for applying what is known as the "cutting-plane method" for producing quality guarantees. You can see a short discussion of how we apply these tools on the Computation page.

For a quick glimpse of the cutting-plane method, here is how I describe the process in a short piece in Scientific American

"The idea is to follow Yogi Berra's advice `When you come to a fork in the road, take it.' A tool called linear programming allows us to do just this, assigning fractions to roads joining pairs of cities, rather than deciding immediately whether to use a road or not. It is perfectly fine, in this model, to send half a salesman along both branches of the fork."

"The process begins with the requirement that, for every city, the fractions assigned to the arriving and departing roads each sum to one. Then, step-by-step, further restrictions are added, each involving sums of fractions assigned to roads. Linear programming eventually points us to the best decision for each road, and thus the shortest possible route."

If you have a few minutes, you can check out the video of the talk Optimal Tours given at the National Museum of Mathematics, where the method is described in detail. Or, keeping with the Korean theme, please have a look at video of the talk Amazon Deliveries, Pub Walks, and Astro Tours, given at KAIST in March 2024.

P vs NP

A great discussion of the P and NP complexity classes, including connections to the TSP, can be found in Lance Fortnow's article Fifty Years of P vs. NP and the Possibility of the Impossible.

Optiland — Credit: https://cacm.acm.org/research/fifty-years-of-p-vs-np-and-the-possibility-of-the-impossible/

The Big Picture

We use large examples of the traveling salesman problem as a means for developing and testing general-purpose optimization methods. The world has limited resources and the aim of the applied mathematics fields of mathematical optimization and operations research is to create tools to help us to use these resources as efficiently as possible.

For general information on mathematical modeling and its impact on industry, commerce, medicine, and the environment, we point you to a number of societies that support mathematics research and education: American Mathematical Society, Mathematical Association of America, Mathematical Optimization Society, INFORMS (operations research), and SIAM (applied mathematics).

Research Team

William Cook, Combinatorics and Optimization, University of Waterloo, Canada
Daniel Espinoza, Alicanto Labs, Chile
Marcos Goycoolea, School of Business, Universidad Adolfo Ibanez, Chile
Keld Helsgaun, Computer Science, Roskilde University, Denmark

Acknowledgements

The huge number of linear-programming models that arose in the computation were solved with the IBM CPLEX Optimizer. Many thanks to IBM for making their great software freely available for academic research.

The map drawings of the tour were created with the Leaflet open-source JavaScript library for mobile-friendly interactive maps and make use of map tiles built by OpenStreetMap, by Carto Basemaps and by Stadia Maps.

We thank Dr. Sang-il Oum, Chief Investigator of the Discrete Mathematics Group at the Institute for Basic Science (IBS) for obtaining the locations of the bars in Korea. The locations were downloaded from a database maintained by the Korean National Police Agency.

The table of point-to-point walking times was created with the Open Source Routing Machine (OSRM).