The infinite series 1/4 + 1/16 + 1/64 + 1/256 + … was one of the first to be summed in the history of mathematics; Archimedes had found by 200 BC that it totals 1/3. There are two neat visual demonstrations that make this fact immediately apparent. In the unit square above, the largest black square has area 1/4, the next-largest black square has area 1/16, and so on. Regions of black, white, and gray make up equal areas in the total figure, so the black squares, taken together, must have area 1/3.

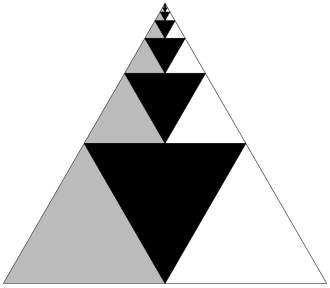
The same argument can be made using triangles (below). If the area of the largest triangle is 1, then the largest black triangle has area 1/4, the next-largest 1/16, and so on. Areas of black, white, and gray make up equal parts of the total figure, so the black regions must total 1/3.