该晦涩的排版符号⍼的起源最近被追溯到1950年的H. Berthold AG字型厂。维基百科用户Moyogo在Berthold 1950年符号目录中发现了该符号,名为“Azimut”(方位角/方向角)。 该符号出现在Berthold 1950-1952年的目录中,但不存在于较早的版本中,包括1946年、1909年和1900年的目录。有趣的是,该字形在视觉上类似于光线通过六分仪的路径——一种用于测量方位角角度的仪器。这种联系强化了符号的命名和预期用途,最终解决了围绕其身份和用途的长期谜团。该发现得益于存档的目录和Mastodon上的一个有帮助的观察。
每日HackerNews RSS
启用 JavaScript 和 Cookie 以继续。
`commandForElement` 和 `command` 属性提供了一种声明式的方法来使按钮具有交互性,而无需大量依赖 JavaScript。 你无需附加事件监听器,只需使用 `commandForElement`(指定目标元素的 ID)将 `<button>` 链接到元素,并使用 `command` 属性定义要执行的操作。 这种方法对于内置命令(如切换弹出框或显示对话框)特别有用,因为它避免了等待 JavaScript 加载,从而提高了初始页面响应速度。 当命令按钮被激活时,将在目标元素上触发 `CommandEvent`。 开发者还可以定义自定义命令(以 `--` 为前缀)并使用 JavaScript 事件监听器处理它们,从而可以控制元素属性,例如旋转,如示例所示。 该系统提供了一种标准化且高效的方法来创建交互式 Web 组件。
我的 ΔE(OK) JND 是多少? 你看到两种颜色。 点击它们之间的线条。 就这样。 一开始很简单。 但不会一直简单。 每一轮颜色都会更接近,直到我们找到你的最小可感知差异——你实际能看到的最小颜色变化。 大约需要 40 轮。 大多数人停留在 0.02 左右。 你可能会做得更好。 你可能不会。 但嘿,证明我错了。 <屏幕清洁剂推荐链接> 开始吧 这是什么? 阅读帖子。
启用 JavaScript 和 Cookie 以继续。
彭博社 需要帮助?请联系我们 我们检测到您的计算机网络存在异常活动 要继续,请点击下面的框来确认您不是机器人。 为什么会发生这种情况? 请确保您的浏览器支持 JavaScript 和 cookies,并且没有阻止它们加载。 有关更多信息,您可以查看我们的服务条款 和 Cookie 政策。 需要帮助? 如需有关此消息的咨询,请联系 我们的支持团队并提供下面的参考ID。 阻止参考ID:96ea7b96-1cc4-11f1-bd3a-9320d3e3c858 使用彭博社订阅,随时掌握最重要的全球市场新闻。 立即订阅
启用 JavaScript 和 Cookie 以继续。
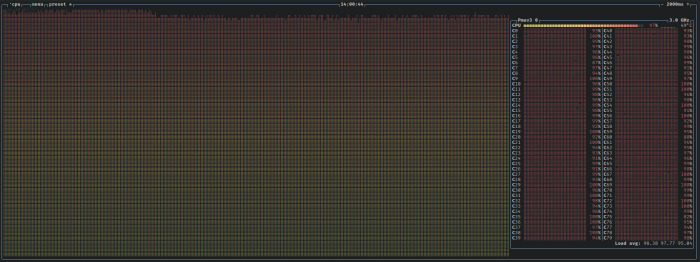 过去三个月,作者一直致力于将 Fedora Linux 移植到 RISC-V 架构。这项工作包括处理错误报告(目前仅剩 17 个)以及提交 86 个软件包构建的补丁请求——其中许多已成功合并并构建为 Fedora 43。
一个主要挑战是由于当前 RISC-V 硬件的限制,构建速度较慢。与其它架构相比(例如,binutils 在 RISC-V 上需要 143 分钟,而在 x86_64 上需要 29 分钟),构建时间显著更长,因此需要禁用链接时优化 (LTO) 以节省内存并缩短构建时间。
作者使用 QEMU 和 80 个模拟核心来缓解这个问题,从而为 LLVM 等复杂软件包实现合理的构建时间。未来的计划包括构建 Fedora 44、标准化内核镜像以及获取更快的硬件——这对 RISC-V 成为 Fedora 的主要架构至关重要。需要更快的构建器来启用 LTO 并实现与其它平台相当的构建时间。
过去三个月,作者一直致力于将 Fedora Linux 移植到 RISC-V 架构。这项工作包括处理错误报告(目前仅剩 17 个)以及提交 86 个软件包构建的补丁请求——其中许多已成功合并并构建为 Fedora 43。
一个主要挑战是由于当前 RISC-V 硬件的限制,构建速度较慢。与其它架构相比(例如,binutils 在 RISC-V 上需要 143 分钟,而在 x86_64 上需要 29 分钟),构建时间显著更长,因此需要禁用链接时优化 (LTO) 以节省内存并缩短构建时间。
作者使用 QEMU 和 80 个模拟核心来缓解这个问题,从而为 LLVM 等复杂软件包实现合理的构建时间。未来的计划包括构建 Fedora 44、标准化内核镜像以及获取更快的硬件——这对 RISC-V 成为 Fedora 的主要架构至关重要。需要更快的构建器来启用 LTO 并实现与其它平台相当的构建时间。
罗宾·斯隆讨论了最近发布的Gemini 3.1 Flash-Lite,称赞其速度、价格和视觉能力——特别是将其集成到更大系统中的潜力,而非直接对话。他指出谷歌持续关注广泛的“通用”智能,这与Anthropic和OpenAI对编码代理的侧重形成对比。 然而,斯隆对谷歌快速淘汰Gemini 3 Pro感到沮丧,强调了依赖外部托管模型的不可靠性。虽然自托管提供了一种解决方案,但目前的选项缺乏Gemini强大的视觉处理能力。他预计这种情况很快就会改变。 这篇来自斯隆个人博客的文章强调了对隐私和速度的承诺,这与印刷品的特性相符。他鼓励读者订阅他的新闻通讯以获取更新。