启用 JavaScript 和 Cookie 以继续。
每日HackerNews RSS
 ## 构建更好的编辑器:一次个人旅程
对现有的文本编辑器感到不满——即使尝试了 Helix、VS Code 和 Vim 等许多编辑器——一位程序员开始构建自己的编辑器。现有工具在对其工作流程至关重要的领域表现不足:高效的项目范围搜索、无缝的 SSH 访问以及功能完善的集成终端。
该项目优先考虑个人需求而非广泛的功能集,专注于为开发人员特定语言和习惯量身定制的简化体验。主要成果包括一个受 Howl 启发的快速文件浏览器、一个高度优化的正则表达式引擎,用于语法高亮和搜索,以及一个基于 Alacritty crate 构建的终端模拟器。通过诸如按需高亮和最小化终端重绘等技术来提高性能。
该开发者强调构建自定义工具的好处:完美适应个人工作流程、加深技术理解、提高生产力,最重要的是,重燃编程的乐趣。这个过程虽然具有挑战性,但却非常有价值,将重点从与工具作斗争转移到创造性问题解决,并重新点燃了对这项技艺的热情。最终,这段经历倡导工程师们拥抱构建自己的工具,在奋斗中找到乐趣,并获得由此带来的个性化力量。
## 构建更好的编辑器:一次个人旅程
对现有的文本编辑器感到不满——即使尝试了 Helix、VS Code 和 Vim 等许多编辑器——一位程序员开始构建自己的编辑器。现有工具在对其工作流程至关重要的领域表现不足:高效的项目范围搜索、无缝的 SSH 访问以及功能完善的集成终端。
该项目优先考虑个人需求而非广泛的功能集,专注于为开发人员特定语言和习惯量身定制的简化体验。主要成果包括一个受 Howl 启发的快速文件浏览器、一个高度优化的正则表达式引擎,用于语法高亮和搜索,以及一个基于 Alacritty crate 构建的终端模拟器。通过诸如按需高亮和最小化终端重绘等技术来提高性能。
该开发者强调构建自定义工具的好处:完美适应个人工作流程、加深技术理解、提高生产力,最重要的是,重燃编程的乐趣。这个过程虽然具有挑战性,但却非常有价值,将重点从与工具作斗争转移到创造性问题解决,并重新点燃了对这项技艺的热情。最终,这段经历倡导工程师们拥抱构建自己的工具,在奋斗中找到乐趣,并获得由此带来的个性化力量。
 这个故事源于1994年的一封邮件,讲述了加利福尼亚州帕洛阿尔托市发生的一起怪异事件。一个城市变压器室,容纳着为市中心办公楼供电的一百万瓦设备,被发现装满了大约2000加仑的废弃食用油。
多年来,附近一家餐厅一直在非法将炸油倾倒进变压器室,错误地认为它通往雨水下水道。变压器的热量使油脂保持熔化状态,造成了严重的火灾隐患。如果变压器过热,可能会点燃油脂,导致一场巨大的“超级油火”。
问题浮出水面是因为餐厅顾客抱怨有腐臭味。城市公用事业部门最终发现了问题,切断了电源,移除了油脂,并更换了变压器。幸运的是,没有人受伤,一家餐厅暂时无法提供油炸食品。
这个故事源于1994年的一封邮件,讲述了加利福尼亚州帕洛阿尔托市发生的一起怪异事件。一个城市变压器室,容纳着为市中心办公楼供电的一百万瓦设备,被发现装满了大约2000加仑的废弃食用油。
多年来,附近一家餐厅一直在非法将炸油倾倒进变压器室,错误地认为它通往雨水下水道。变压器的热量使油脂保持熔化状态,造成了严重的火灾隐患。如果变压器过热,可能会点燃油脂,导致一场巨大的“超级油火”。
问题浮出水面是因为餐厅顾客抱怨有腐臭味。城市公用事业部门最终发现了问题,切断了电源,移除了油脂,并更换了变压器。幸运的是,没有人受伤,一家餐厅暂时无法提供油炸食品。
## Zig 开发更新 - 2026 (截至 3 月 10 日) 最近的 Zig 开发主要集中在重要的内部改进和扩展功能上。一个包含 30,000 行代码的 PR 彻底修改了编译器的类型解析逻辑,从而实现了更快的增量编译(修复了过度分析问题),并允许编译器在分析未使用的类型字段时“更懒”——这对于用作命名空间的类型是有益的。依赖循环错误信息也得到了显著改进,提供了清晰的解决指导。 在标准库方面,`std.Io.Evented` 接近完成,为 I/O 操作提供用户空间堆栈切换(纤程/协程),但仍被认为是实验性的。努力仍在优先使用原生 Windows API 而不是 Win32 包装器,以提高性能和可靠性,避免不必要的分配和故障。 `zig libc` 子项目正在取得进展,用 Zig 包装器替换了 vendored C 代码,用于 libc 函数,从而减少了代码重复并提高了编译速度。这也为未来与 Zig 功能(如 io_uring 和资源泄漏检测)集成打开了可能性。已经删除了超过 250 个 C 文件。 最后,团队承认并表示与在城市中面临问题的抗议者站在一起。
请启用 JavaScript 并禁用任何广告拦截器。

## Bippy:React 内部机制探索 Bippy 是一套工具,用于访问 React 的内部“fiber”——代表组件和 DOM 元素的执行核心单元——而无需修改 React 代码本身。通常,这些内部机制是无法访问的,但 Bippy 通过伪装成 React Devtools 来绕过这一限制,从而访问 fiber 树和相关数据。它支持 React 17-19 版本,并且不需要事先了解 React 的源代码。 主要功能包括遍历 fiber 树(`traverseFiber`)、识别渲染的组件(`traverseRenderedFibers`)以及检查 props、state 和 context。Bippy 通过拦截 React 与 `window.__REACT_DEVTOOLS_GLOBAL_HOOK__` 对象的通信来实现这一点,该对象传统上由 React Devtools 使用。 **使用方法:** 在 React 之前导入 Bippy,以接入其内部机制。像 `instrument` 这样的函数可以安全地修补全局 hook,而 `secure` 则添加了错误处理。像 `getFiberFromHostInstance` 这样的工具可以将 DOM 元素链接到其对应的 fiber。 **重要提示:** Bippy 主要是一个开发工具。虽然提供了安全保障,但在生产环境中使用时应谨慎考虑,并参考 React-Scan 等项目以实现更强大的功能。它是一个强大的工具,用于理解 React 的内部运作和调试复杂应用程序。
## 保护光标云代理中的密钥 光标云代理虽然简化了工程工作流程,但也带来了新的凭证泄露风险。每个代理都在隔离的虚拟机中运行,需要密钥才能执行诸如数据库访问和私有包安装等任务。常见的陷阱——硬编码凭证、将密钥存储在提交的文件中以及烘焙在快照数据中——都会产生漏洞。 Infisical 提出了一种解决方案:**仅将 Infisical 机器身份凭证存储在光标的密钥 UI 中。** 然后使用这些凭证在运行时从 Infisical 动态拉取所有其他密钥,从而避免将其存储在光标内部。 这可以通过使用 `infisical run` 将密钥作为环境变量直接注入到进程中,或使用 `infisical export` 将密钥写入必要的文件(如 `.env`)来实现。 重要的是,这种方法确保密钥在每次启动时都是最新的、可审计的并且可以轮换。 此外,Infisical 建议将机器身份限定到特定环境(开发、生产、CI),并具有有限的访问权限,从而最大限度地减少潜在泄露的影响范围。 通过最大限度地减少光标中存储的内容并利用像 Infisical 这样强大的密钥管理系统,团队可以保护其代理并避免烘焙在其中的、长期存在的凭证带来的风险。
## 生成模型:一种科学的实用性方法 当前关于生成模型的讨论,常常缺乏对其实用性的严格、科学评估。与其通过建模工具和任务来分析工具X是否对任务Y有用,不如基于“感觉”和广泛的应用来做出声明,而缺乏批判性评估。作者提出一个基于三个关键因素来评估生成模型实用性的框架:**编码成本**、**验证成本**以及**过程与成果**的重要性。 **编码成本**比较了提示模型与直接创建所需输出的努力程度。**验证成本**评估了确保生成结果满足要求的难度。最后,**过程**的重要性认识到,某些任务,例如教育或某些工程实践,优先考虑*如何*做,而不仅仅是*做什么*。 作者认为,当编码成本低廉和/或验证非常容易,*并且*过程不重要时,实用性会增加。复杂的任务通常会增加编码和验证成本,从而降低实用性。此外,生成模型不太可能对依赖过程的任务有帮助。 最终,确定实用性需要领域专业知识以及对这些权衡的仔细考虑——这是一种工程形式。虽然承认这些模型的潜力,但作者强调“合理”的输出并不等同于“有用”的输出,并且增加模型复杂度并不能自动转化为增加价值。
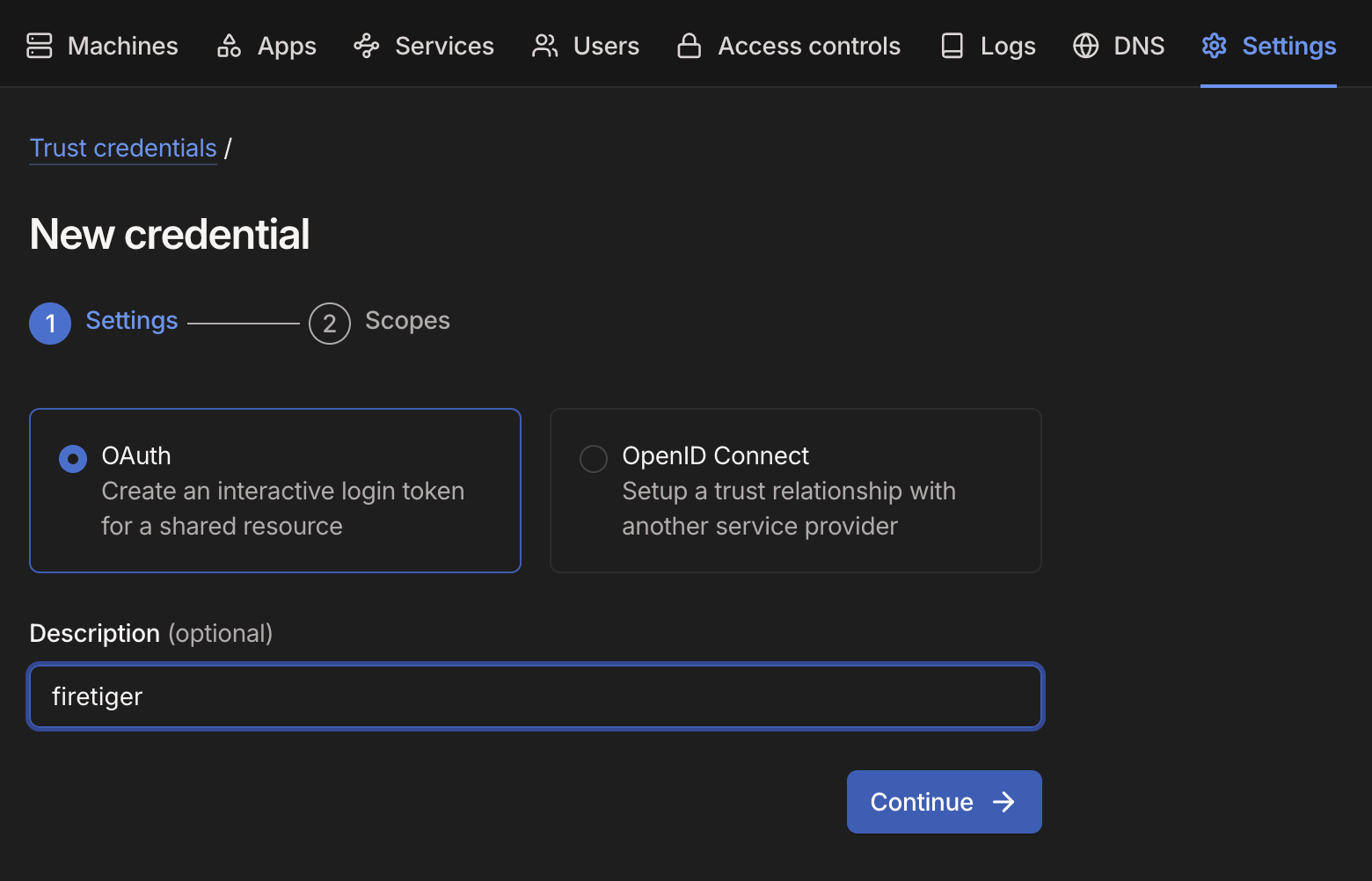 ## Firetiger 现在可以连接到您的私有数据库
Firetiger 数据库代理旨在自动化数据库管理(Postgres、MySQL、ClickHouse),但大多数有价值的数据库都位于私有网络中,这带来了连接性挑战。传统的解决方案,如 VPC 对等互联或 VPN,复杂且容易出现问题。
Firetiger 通过 **网络传输** 来解决这个问题,首先是 **Tailscale**。Tailscale 简化了网络之间的安全连接,允许 Firetiger 代理访问您的数据库,*而无需*将其暴露到公共互联网。
操作方式如下:您使用 Tailscale 的基于身份的访问控制在您的 Tailnet 中授予 Firetiger 访问权限,创建凭据,并配置 Firetiger Tailscale 网络传输。这将建立一个安全加密的连接。
这意味着您现在可以利用 Firetiger 的自动化 DBA 和自定义代理来监控和管理您私有托管的数据库,消除盲点并简化操作——即使在复杂的网络配置下也是如此。提供了一个详细的指南,其中包含完整的设置示例。
## Firetiger 现在可以连接到您的私有数据库
Firetiger 数据库代理旨在自动化数据库管理(Postgres、MySQL、ClickHouse),但大多数有价值的数据库都位于私有网络中,这带来了连接性挑战。传统的解决方案,如 VPC 对等互联或 VPN,复杂且容易出现问题。
Firetiger 通过 **网络传输** 来解决这个问题,首先是 **Tailscale**。Tailscale 简化了网络之间的安全连接,允许 Firetiger 代理访问您的数据库,*而无需*将其暴露到公共互联网。
操作方式如下:您使用 Tailscale 的基于身份的访问控制在您的 Tailnet 中授予 Firetiger 访问权限,创建凭据,并配置 Firetiger Tailscale 网络传输。这将建立一个安全加密的连接。
这意味着您现在可以利用 Firetiger 的自动化 DBA 和自定义代理来监控和管理您私有托管的数据库,消除盲点并简化操作——即使在复杂的网络配置下也是如此。提供了一个详细的指南,其中包含完整的设置示例。